The main dataset used is the flights dataset. It contains the US domestic flights in January 2020 [1]. The other two datasets used are fabricated datasets created for the purpose of this guide.
The link to the recording of this workshop can be found here. Additional resources are listed below. If you need assistance, fill out the support request form.
TABLE OF CONTENTS
Importing Data
Exploring Data
Graphs
New Variables
Managing Data
Resources
Importing Data
Working directory
The directory is the place on your computer that is the home for R; therefore, this is where R is saving files and also where R is looking for files. Because R might be using a folder buried deep in your computer’s hard drive, there are two ways of finding and setting your working directory. First, you can use getwd() to find the current directory and setwd() to set the directory to a different path. NOTE: need to use the forward (/) instead of the backward slash (\) for directory paths in R.
getwd()
setwd("/Users/nadia/Desktop")The second way is by going under File on the menu bar and going down to Change dir. This way is best if you do not know the exact name and location of where you want to set your new working directory because it allows you to go through all of the files on your computer.
Importing Data
DATA: flights.csv
Download the flights dataset by clicking on the link above or using the url uoft.me/flightscsv.
Use read.csv() to read csv files. Set the header option to true if the file has column titles and false otherwise. The default option is always true.
flights<-read.csv("January 2020 Flights.csv")
Exploring Data
Unless you opened the .csv file beforehand, you don’t know much about the information you just loaded into R. To find out more, use the dim() function to find out the dimension of a data set. To view to contents of a dataset, use the str() function. The head() function displays the first six rows of the dataset and tail() displays the last six rows.
str(flights) head(flights) tail(flights)


To open or, in R terminology, print the content of a data set or a variable in the R-console, simply write the data set or the variable. A data set has 2 dimensions. The first dimension is the row number and the second dimension is the column number. The two dimensions are separated by a comma. For example, ont14[1,2] prints the value in the first row and second column of the ont14 data set, ont14[1, ] prints the first row and ont14[,2] prints the second column. As you may notice, we use square brackets when isolating data and round brackets when working with functions. To print a range of rows or a range of columns, indicate the range separated by a colon.
flights[1,5]
flights[1,"originstate"]
flights[1, 1:5]
flights[1000:1005,c("originstate", "deptime", "depdelay")]

When we type a variable by itself, it gives us an error message. To access a variable, use the dollar sign “$”. For example, flights$originstate returns the originstate variable.
originstate flights$originstate
Frequency Tables
The table() function can be used to make a frequency table. You will also find functions from external packages that can be used to make frequency tables.
The table() function can be used to make a frequency table. You will also find functions from external packages that can be used to make frequency tables.
table(flights$depdelay) table(flights$depdelay, exclude=NULL)
You can use the CrossTable() function from the gmodels package to make a two-way frequency table. First, you need to install the gmodels package using the install.packages() function and load it using the library() function.
install.packages("gmodels")
library(gmodels)
CrossTable(flights$depdelay, flights$arrdelay)

Descriptive Statistics
The summary() gives a summary of the object. If the object is a data set, it gives a summary of all the variables in a data set and if it is a variable, it gives a summary of the variable. Other descriptions can be obtained using the fivenum(), min(), mean(), max(), var(), quantile() functions.
summary(flights$distance) summary(flights) mean(flights$distance) sd(flights$distance)
The by() function can be used to view the average candidate approval rates by another category. For example, below, we can see the average approval rates by income category.
summary(flights$distance[flights$dayofweek==1]) by(flights$distance, flights$dayofweek, summary)
Graphs
The following codes can be used to make bar charts, pie charts, boxplots and scatterplots. These are just a few of the many data visualizations you can produce using R. Each example shows you how to add more information to better develop the data visualization, so the below images are made using the last code in the entry.
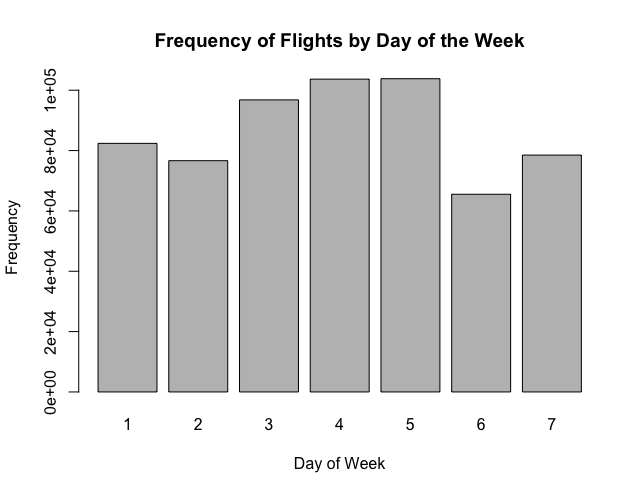
Bar chart
# Bar chart dayofweektable <- table(flights$dayofweek) barplot(dayofweektable) barplot(dayofweektable, main="Frequency of Flights by Day of the Week", xlab="Day of Week", ylab="Frequency")
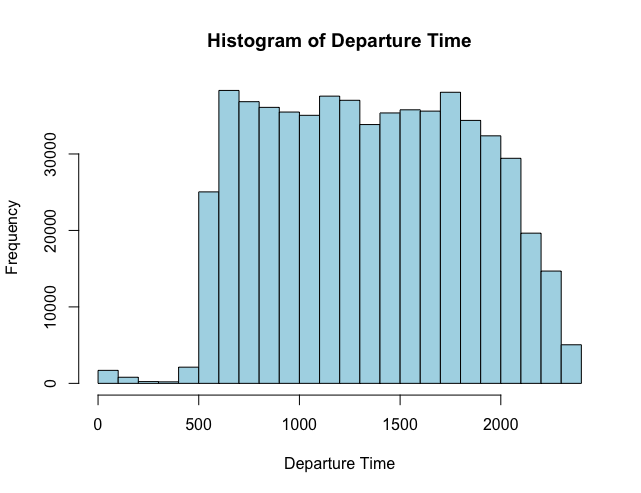
Histogram
hist(flights$deptime) hist(flights$deptime, main="Histogram of Departure Time", xlab="Departure Time", col="lightblue")
Scatterplot
plot(flights$dayofweek, flights$deptime) plot(flights$dayofweek, flights$deptime, pch=3, cex=3, col="darkred")
New Variables
To generate a new variable that is a combination of other variables, assign the combination to a new variable name.
# Example 1 flights$distancemiles <- flights$distance*0.621 summary(flights$distance) summary(flights$distancemiles)

# Example 2 flights$instate<-NA flights$instate[flights$originstate==flights$deststate] <- 1 flights$instate[flights$originstate!=flights$deststate] <- 0 CrossTable(flights$instate)

# Example 3
flights$delay <- ""
flights$delay[flights$depdelay==0 & flights$arrdelay==0] <- "not delayed"
flights$delay[flights$depdelay==1 & flights$arrdelay==0] <- "delayed at departure"
flights$delay[flights$depdelay==0 & flights$arrdelay==1] <- "delayed at arrival"
flights$delay[flights$depdelay==1 & flights$arrdelay==1] <- "delayed at both"
CrossTable(flights$delay)
flights$delay <- factor(flights$delay,
levels = c("","not delayed", "delayed at departure", "delayed at arrival", "delayed at both"),
ordered=TRUE)
CrossTable(flights$delay

Save() can be used to save a dataset as a native R .RData data file.
save(flights, file="Flights 2020.RData")
Managing Data
Subsetting Data
To subset, use the subset() function.
Example 1
departure<-subset(flights, select=c(originstate, origin, deptime, depdelay, deststate))
dim(departure)

Example 2
hawaii<-subset(flights, flights$deststate=="Hawaii" & flights$dayofmonth==1) dim(hawaii)
DATA: airlinecodes.csv
Download the airlines dataset by clicking on the link above or using the url uoft.me/airlinescsv.
Merging Data
To combine two datasets, you can use the merge() function.
airlinecodes <- read.csv("airlinecodes.csv")
flightsmerged <- merge(airlinecodes, flights, by="carrier")
CrossTable(flightsmerged$airline, flightsmerged$diverted)

Converting to Data Frame
A data frame is a dataset. To convert output from a function to a data frame, you can use the as.data.frame() function.
origin<-as.data.frame(table(flights$origin))
names(origin)<-c("code", "origin")
dest<-as.data.frame(table(flights$dest))
names(dest)<-c("code", "dest")
airports <-merge(origin, dest, by="code", all=TRUE)
str(airports)

Exporting Data
To export a dataset to a CSV file, you can use the write.csv() function.
write.csv(airports, file="Airports.csv", row.names=FALSE)
Resources
[1] The flights dataset is modified from the original version on the Kraggle website.
[2] The tutorial code and the workshop Powerpoint presentation can be downloaded from here.
[3] You can enroll in the introductory R Quercus course here.